
全部
▼
搜索
熱搜:
位置:中冶有色 >
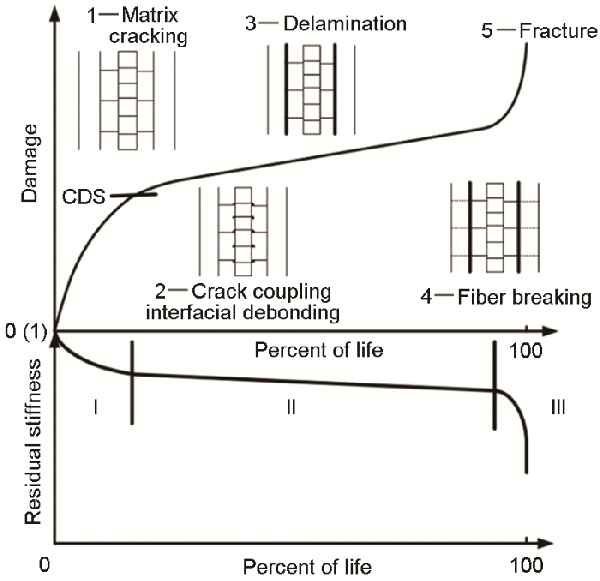
> 考慮溫度和纖維含量影響的單向?qū)雍习宀牧系耐嘶P?/p>
 844
編輯:中冶有色技術(shù)網(wǎng)
來(lái)源:吳一凡,溫衛(wèi)東,崔海濤,張宏建
844
編輯:中冶有色技術(shù)網(wǎng)
來(lái)源:吳一凡,溫衛(wèi)東,崔海濤,張宏建
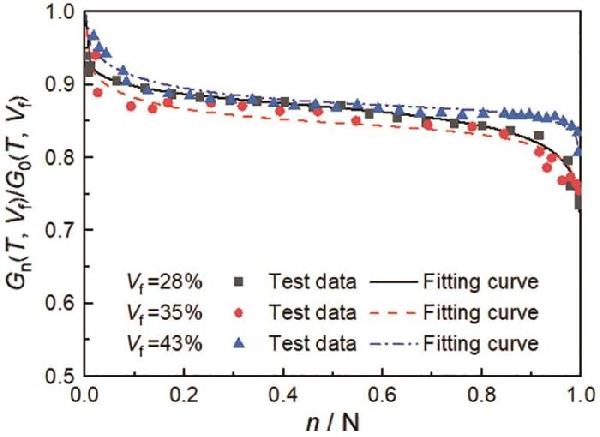
| Stacking sequence | Vf/% | T/℃ |
|---|---|---|
| [45/-45]2S | 28 | 20 |
| [45/-45]3S | 35 | 20 |
| [45/-45]4S | 43 | 20 |

|
Fitting parameter |
Fitting results |
Fitting parameter |
Fitting results |
|---|---|---|---|
| k1 | 1.36 | k6 | 1.34 |
| k2 | -0.76 | k7 | 1.47 |
| k3 | -18.21 | k8 | 0.72 |
| k4 | 12.22 | c1 | 0.71 |
| k5 | -2.3 | c2 | 0.01 |
| Fitting parameter | Fitting results |
|---|---|
| w | 0.9042 |


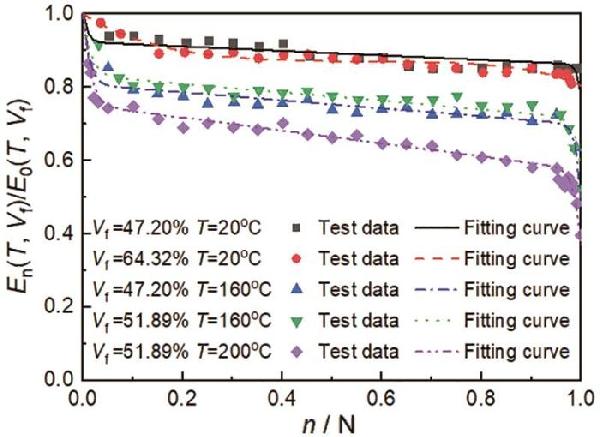
| Stacking sequence | Vf/% | Temperature/℃ |
|---|---|---|
| [0]8 | 47.20 | 20 |
| [0]8 | 47.20 | 160 |
| [0]12 | 51.89 | 160 |
| [0]12 | 51.89 | 200 |
| [0]16 | 64.32 | 20 |

|
Fitting parameter |
Fitting results |
Fitting parameter |
Fitting results |
|---|---|---|---|
| k1 | -5.11 | k7 | 10.1 |
| k2 | 2.56 | k8 | -10.11 |
| k3 | 13 | c1 | 1.065 |
| k4 | -10.88 | c2 | 1.318 |
| k5 | 2.06 | k | 0.25 |
| k6 | -0.1 | Tr | -42.49 |
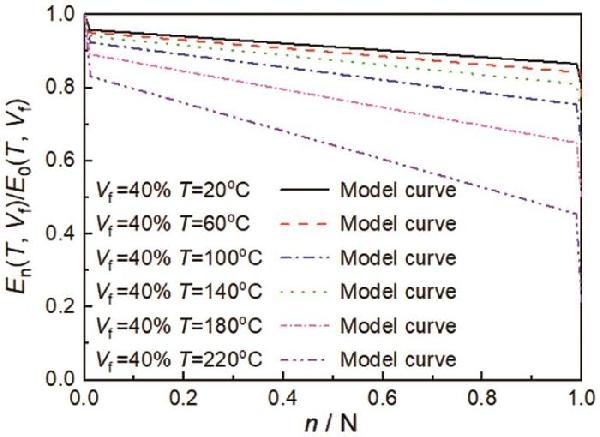

| Fitting parameter | Fitting results |
|---|---|
| w | 1.75 |
| t | 25.37×10-3 |
| s | 25.11×10-4 |

 分享 0
分享 0
 舉報(bào) 0
舉報(bào) 0
 收藏 0
收藏 0
 反對(duì) 0
反對(duì) 0
 點(diǎn)贊 0
點(diǎn)贊 0

 中冶有色技術(shù)平臺(tái)
中冶有色技術(shù)平臺(tái) 2024年12月27日 ~ 29日
2024年12月27日 ~ 29日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年01月03日 ~ 05日
2025年01月03日 ~ 05日  2025年03月25日 ~ 27日
2025年03月25日 ~ 27日  2025年04月27日 ~ 29日
2025年04月27日 ~ 29日 
