鈦合金的比強(qiáng)度高、高溫性能優(yōu)異、焊接性能良好以及耐腐蝕性能出色，在航空航天、海洋船舶、能源化工以及生物醫(yī)療等領(lǐng)域得到了廣泛的應(yīng)用 但是，部分鈦合金存在室溫蠕變，即在室溫下保持載荷(保載)產(chǎn)生的塑性應(yīng)變隨時間不斷累積 在鈦合金的服役過程中，結(jié)構(gòu)件可能經(jīng)歷較長時間的保載過程，如潛水器在水下長時間作業(yè)以及航空器的巡航等 在室溫下即使施加的保載應(yīng)力低于名義屈服強(qiáng)度σp0.2，與其他金屬材料相比，純鈦和部分鈦合金依然發(fā)生較為明顯的蠕變效應(yīng)[1~9] 這些鈦合金有α型和α+β型鈦合金，例如TA7(Ti-5Al-2.5Sn[6])，TA19(Ti-6Al-2Sn-4Zr-2Mo[7])，TC4(Ti-6Al-4V[5, 8])以及Ti6211(Ti-6Al-2Nb-1Ta-0.8Mo[9])等含有密排六方結(jié)構(gòu)α相的鈦合金，而只含體心立方結(jié)構(gòu)β相的β型鈦合金的室溫蠕變可忽略不計[2,10~12] 鈦合金在低于屈服強(qiáng)度的室溫蠕變，通常觀察到蠕變的第一階段[1,5~7,9]，亦稱初始蠕變(Primary creep)階段、瞬態(tài)蠕變(Transient creep)階段或減速蠕變階段[1,7,9,13] 鈦合金的室溫蠕變不僅影響結(jié)構(gòu)件的尺寸精度，造成應(yīng)力松弛，影響結(jié)構(gòu)件安全有效的服役[1, 2]，室溫蠕變引入的塑性應(yīng)變還可能影響結(jié)構(gòu)件的后續(xù)使用性能，比如疲勞性能[14]，造成蠕變的二次危害

保載疲勞是一種在三角波疲勞峰值載荷處引入保載過程產(chǎn)生的梯形波疲勞[14,15] 部分鈦合金在室溫保載時產(chǎn)生顯著的蠕變應(yīng)變，因此與對應(yīng)參數(shù)下的三角波疲勞相比，這些合金的保載疲勞通常呈現(xiàn)出更快和更大的塑性應(yīng)變累積[16,17] 同時，與對應(yīng)參數(shù)下的三角波疲勞相比，這些鈦合金的保載疲勞壽命(斷裂周次)顯著降低，有時可達(dá)一個數(shù)量級以上[15,17]，這種現(xiàn)象稱為保載效應(yīng) 有學(xué)者把鈦合金室溫疲勞的保載效應(yīng)歸因于保載疲勞中更為顯著的塑性應(yīng)變累積[14~16,18~21]，即認(rèn)為保載疲勞中累積的塑性應(yīng)變能加速疲勞損傷，而鈦合金室溫保載疲勞的塑性應(yīng)變累積主要來源于室溫蠕變 因此，鈦合金的室溫蠕變非常值得研究

自1949年H. Andenstedt發(fā)現(xiàn)純鈦發(fā)生室溫蠕變以來[22]，很多學(xué)者對鈦及鈦合金的室溫蠕變進(jìn)行了深入研究 W. H. Miller等[9] 研究了Ti6211合金的組織對其室溫蠕變性能的影響 結(jié)果表明：與網(wǎng)籃組織相比，魏氏組織中集束結(jié)構(gòu)的尺寸較大，而其中的α相取向相同 α相與β相之間符合Burgers取向關(guān)系，位錯的滑移可在整個集束結(jié)構(gòu)中進(jìn)行 因此，魏氏組織提供了更長的滑移距離，使其具有較高的室溫蠕變速率和蠕變變形量 而馬氏體組織中片層之間的取向不同，界面成為滑移的障礙，使相同蠕變條件下馬氏體組織的蠕變量最小 S. Ankem等[23] 研究了Ti-8.1V合金的組織對其室溫蠕變性能的影響 結(jié)果表明：在晶粒尺寸相同的條件下，等軸組織的室溫蠕變性能優(yōu)于魏氏組織 有關(guān)學(xué)者研究了Ti-1.6V[24], Ti-9.4Mn[10], Ti-14.8V[11]等鈦合金的晶粒尺寸對其室溫蠕變性能的影響 結(jié)果表明，合金的晶粒尺寸越小其室溫蠕變性能越好 與高溫蠕變時晶界作為材料中有害因素的情況相反，室溫蠕變時晶界成為滑移以及孿生變形的障礙 因此，鈦合金的晶粒越細(xì)、晶界越多，其室溫蠕變性能越好 很多學(xué)者研究了應(yīng)力水平對鈦合金室溫蠕變的影響[1,2,5~7,9,24] 應(yīng)力水平影響鈦合金室溫蠕變的規(guī)律也容易理解：蠕變應(yīng)力水平越低、蠕變效應(yīng)越弱，蠕變應(yīng)力低至一定程度(蠕變應(yīng)力門檻值[1])時蠕變效應(yīng)消失 以往關(guān)于鈦合金材料蠕變應(yīng)力方面的研究，主要關(guān)注在各個應(yīng)力水平下蠕變的定量化，很少測試材料蠕變應(yīng)力的門檻值 S. Ankem等提出了鈦及鈦合金室溫蠕變的微觀變形機(jī)制[25,26]：單相α鈦合金和單相β鈦合金中主要為滑移以及具有時間依賴性的孿生；在α+β兩相鈦合金中為α相中的滑移和孿生，相間界面滑移以及β相中的應(yīng)力誘發(fā)馬氏體相變等 目前國內(nèi)外對鈦合金室溫蠕變的研究，主要集中在顯微組織和應(yīng)力水平對不同鈦合金室溫蠕變的影響，以及室溫蠕變的微觀變形機(jī)制[1,5~7,9,13,27, 28] 鑒于此，本文參照文獻(xiàn)[1]設(shè)計一種階梯升力蠕變實驗，研究不同應(yīng)力水平下的蠕變并測試合金的蠕變應(yīng)力門檻值，研究宏觀織構(gòu)、應(yīng)力水平和預(yù)塑性應(yīng)變等因素對Ti-6Al-4V軋制板材室溫蠕變的影響以及已發(fā)生的室溫蠕變對材料后續(xù)的蠕變性能和疲勞性能的影響

1 實驗方法

實驗用試樣均取自一塊板厚(符號為H)為72 mm的Ti-6Al-4V軋制板材 出于深海高壓的工程應(yīng)用背景，文中側(cè)重于壓縮實驗，因此試樣規(guī)格的設(shè)計參考了GB/T 7314-2005《金屬材料室溫壓縮試驗方法》 無論壓縮還是拉伸，本文中所有實驗(單調(diào)加載實驗、蠕變實驗以及疲勞實驗)用樣的尺寸均統(tǒng)一為圖1a所示的規(guī)格，試樣平行段的尺寸為?6 mm× 14 mm

圖1



圖1試樣的規(guī)格和取樣示意圖

Fig.1Size of specimens (a) and sampling diagram (b) (unit: mm)

在研究宏觀織構(gòu)對Ti-6Al-4V室溫蠕變性能的影響時，需要抽取不同方向的試樣，圖1b為其取樣示意圖 抽取RD(軋向)或TD(橫向)試樣時，沿板厚方向每12 mm抽取一排，從表層到心部正好取得3排試樣，分別命名為表層(0H)、亞表層(0.25H)和心部(0.5H)試樣 沿板材厚度方向以中截面為對稱面將軋制板材上下部分視為對稱，文中不再區(qū)分上下表層和上下亞表層 考慮到試樣的尺寸(圖1a)，抽取ND(板厚方向)試樣時只能抽取一個位置變量的ND試樣，且其平行段位于板厚方向的心部，因此命名為ND 0.5H

采用控制變量法，研究應(yīng)力水平、預(yù)塑性應(yīng)變對Ti-6Al-4V室溫蠕變性能的影響以及室溫蠕變對合金后續(xù)蠕變以及疲勞性能的影響，為使材料學(xué)變量只有一個，本文在這些實驗中統(tǒng)一采用只能抽取一個位置變量的ND試樣，即ND 0.5H

無論是壓縮還是拉伸，所有測試力學(xué)性能的實驗(單調(diào)加載實驗、蠕變實驗以及疲勞實驗)都在Instron 8801上進(jìn)行，使用機(jī)器附帶的軸向引伸計測量和控制應(yīng)變，實驗環(huán)境均為室溫大氣環(huán)境 室溫單調(diào)壓縮和單調(diào)拉伸實驗全程采用恒應(yīng)變速率的控制模式，參數(shù)的設(shè)定分別參考國標(biāo)GB/T 7314-2005《金屬材料室溫壓縮試驗方法》和GB/T 228.1-2010《金屬材料拉伸試驗第1部分：室溫試驗方法》，單調(diào)壓縮實驗的應(yīng)變速率為0.8×10-4/s，單調(diào)拉伸實驗的應(yīng)變速率為2.5×10-4/s 在單調(diào)壓縮實驗中，由于試樣在壓縮過程中應(yīng)力逐漸偏離單軸壓縮狀態(tài)，伴隨著試樣快速發(fā)生屈曲失穩(wěn)斷裂風(fēng)險的加劇，為了避免機(jī)器夾頭在高壓狀態(tài)下發(fā)生碰撞，在總應(yīng)變達(dá)到4%時即終止實驗 蠕變和疲勞實驗，均采取載荷控制的方式 由于不同方向試樣間的屈服強(qiáng)度差異過大(可達(dá)150 MPa以上，見表1)，在設(shè)定普通蠕變的蠕變應(yīng)力以及保載疲勞的峰值應(yīng)力時進(jìn)行了歸一化處理，均采用試樣各自屈服強(qiáng)度σy(由該位置平行樣的單調(diào)加載實驗獲取)的0.95倍，即σmax=0.95σy 普通蠕變和保載疲勞的加載波形的示意圖如圖2所示，其中加卸載時間均為1 s，普通蠕變的保載時間大于100 h，保載疲勞每周次的保載時間為120 s，應(yīng)力比R = 0 對于三角波高周疲勞(HCF)，σmax=0.8σy或0.95σy，應(yīng)力比R=0，疲勞波形為三角波，疲勞頻率f為10 Hz

Table 1

表1

表1Ti-6Al-4V軋制板材各向各層單調(diào)壓縮性能(平行樣數(shù)量為2)

Table 1Compressive properties of the rolled Ti-6Al-4V plate (the number of parallel samples is 2)

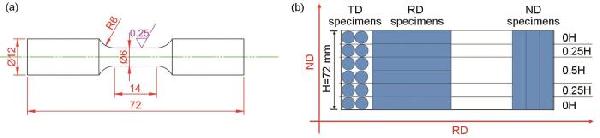
	σy / MPa	E / GPa	n	<0001> peak pole density
ND 0.5H	857	111.2	0.023	-
TD 0H	1016	129.5	0.047	3.15
TD 0.25H	979	129.2	0.038	2.08
TD 0.5H	955	128.8	0.051	5
RD 0H	905	120.6	0.039	-
RD 0.25H	908	123.1	0.043	1.28
RD 0.5H	917	124.6	0.046	2.08

圖2



圖2普通蠕變和保載疲勞的加載波形

Fig.2Test waveforms of normal creep (a) and dwell fatigue (b)

出于工程應(yīng)用背景的需要，本文研究織構(gòu)對合金室溫力學(xué)性能(單調(diào)加載、蠕變以及保載疲勞)的影響時，均采用壓應(yīng)力 研究應(yīng)力水平、預(yù)塑性應(yīng)變對合金蠕變性能的影響時，對壓應(yīng)力、拉應(yīng)力的情況進(jìn)行了實驗并進(jìn)行對比 研究已發(fā)生的蠕變對合金后續(xù)疲勞性能的影響時，為了避免壓應(yīng)力下疲勞試樣斷裂時機(jī)器夾頭在高壓狀態(tài)下發(fā)生碰撞，只測試?yán)瓚?yīng)力的情況 原則上，相對于拉應(yīng)力拉應(yīng)變，壓應(yīng)力壓應(yīng)變?nèi)藶榧s定的符號為負(fù)號，但文中大部分實驗為壓應(yīng)力下的實驗，同時為了方便觀察以及對比拉壓，本文中的壓應(yīng)力壓應(yīng)變也全部換算成正號

顯微組織和宏觀織構(gòu)表征樣，均在各厚度層的中心位置切取 用于表征顯微組織的試樣經(jīng)150#、800#和2000#砂紙磨光后使用二氧化硅懸濁液拋光，然后用體積比為HF∶HNO3∶H2O=1∶3∶96的Kroll試劑腐蝕，最后用金相顯微鏡ZEISS Axiovert 200 MAT觀察金相顯微組織 用于表征宏觀織構(gòu)的試樣經(jīng)150#、800#和2000#砂紙磨光后用無水乙醇沖洗干凈，做好方向標(biāo)記后用D8 Discover X射線衍射儀測試織構(gòu)

2 結(jié)果和討論2.1 織構(gòu)對室溫蠕變的影響

在軋制板材過程中組織和織構(gòu)可能不均勻，從而使材料的力學(xué)性能不均勻，因此研究室溫蠕變和保載疲勞性能前，表征和測試鈦合金軋制板材的組織、織構(gòu)和基本力學(xué)性能(如單調(diào)加載性能)，以對板材的組織、織構(gòu)和力學(xué)性能形成基本的認(rèn)識，為后續(xù)室溫蠕變以及保載疲勞實驗的設(shè)計和分析做準(zhǔn)備

本文實驗用Ti-6Al-4V軋制板材各處的組織均為短棒狀，差異并不顯著(圖3)，因此本文只研究織構(gòu)對Ti-6Al-4V室溫蠕變性能的影響

圖3



圖3Ti-6Al-4V軋制板材從表層到心部的顯微組織

Fig.3Microstructures of the rolled Ti-6Al-4V plate at (a) 0H, 0.25H (b) and 0.5H (c)

織構(gòu)是多晶材料中晶粒發(fā)生擇優(yōu)取向而偏離隨機(jī)分布的結(jié)果，織構(gòu)使多晶材料的力學(xué)性能產(chǎn)生各向異性 鈦合金中的α相屬于密排六方(Hexagonal Close-Packed, HCP)結(jié)構(gòu)，其對稱性比面心立方(FCC)和體心立方(BCC)等晶體結(jié)構(gòu)更低，容易開動的滑移系有限，因此在軋制等塑性成型階段α晶粒容易朝著相同的宏觀方向轉(zhuǎn)動，即發(fā)生擇優(yōu)取向而形成織構(gòu) 在α相含量較高的鈦合金(α鈦合金、近α鈦合金以及部分α+β鈦合金)軋制板材中，常見的織構(gòu)有α晶粒的c軸(晶向<0001>)集中趨向平行于軋制板材橫向TD的T型織構(gòu)和α晶粒的c軸集中趨向平行于軋制板材法向ND的B型織構(gòu)[29,30]

密排六方晶粒沿著不同的方向，其力學(xué)性能的差異較大 在微觀上，當(dāng)單獨的α晶粒c軸與應(yīng)力軸平行時，晶粒內(nèi)部可動滑移系的施密特因子較小，此時晶粒的變形難度最大 這種晶粒，稱為硬取向晶粒；反之，當(dāng)α晶粒的c軸與應(yīng)力軸的夾角接近45°時，晶粒內(nèi)部可動滑移系的施密特因子大，晶粒的變形難度小 這種晶粒，稱為軟取向晶粒[16,31~33] 在宏觀上，試樣的<0001>基面織構(gòu)與外加載荷的方向一致時，試樣的變形難度最大，則其與強(qiáng)度相關(guān)的各力學(xué)性能會偏高

2.1.1 織構(gòu)的表征

為了研究織構(gòu)對Ti-6Al-4V軋制板材室溫蠕變性能的影響，需要表征和分析板材的織構(gòu) 圖4給出了Ti-6Al-4V軋制板材(0001)極圖從表層到心部的變化 從圖4a可以看出，板材表層α相晶粒的<0001>晶向趨向于指向TD附近，峰值極密度值約為3.15，即形成了T型織構(gòu) 圖4b表明，板材亞表層α相晶粒的<0001>晶向從TD向RD發(fā)散，α相晶粒的<0001>晶向不再只集中指向TD，而是散布在TD-RD平面上，并且極密度的值從TD到RD逐漸降低 這種取向的發(fā)散，使TD方向上<0001>晶向的峰值極密度值降低到2.08附近 圖4c則表明，板材心部α相晶粒的<0001>晶向取向的發(fā)散達(dá)到兩極化，并在TD和RD兩個方向上集中，<0001>晶向的極密度值在TD和RD兩個方向附近均出現(xiàn)極值，分別約為5和2.08 綜上所述，在軋制板材的表層形成了T型織構(gòu)，由表層到心部，<0001>晶向的取向由TD向RD發(fā)散，最后在心部形成了<0001>晶向分別沿TD和RD集中分布的兩套織構(gòu)

圖4



圖4Ti-6Al-4V軋制板材從表層到心部的(0001)極圖

Fig.4(0001) pole figures of the rolled Ti-6Al-4V plate at 0H (a), 0.25H (b) and 0.5H (c)

2.1.2 室溫單調(diào)壓縮性能

考慮到織構(gòu)使合金力學(xué)性能產(chǎn)生不均勻性，在設(shè)計室溫壓縮蠕變實驗的參數(shù)前，先測試和分析了Ti-6Al-4V軋制板材各向各層試樣的單調(diào)壓縮性能 圖5a給出了Ti-6Al-4V軋制板材各向各層試樣單調(diào)壓縮時真應(yīng)力-應(yīng)變曲線的差異 可以看出，彈性變形階段屬于線彈性變形，可用Hooke定律(式1)描述此階段應(yīng)力-應(yīng)變的關(guān)系

σ=E×ε

(1)

其中E為彈性模量，σ與ε分別為真應(yīng)力和真應(yīng)變 圖5b則分別給出了Ti-6Al-4V軋制板材各向各層試樣的單調(diào)壓縮真應(yīng)力-塑性應(yīng)變曲線 可以看出，在雙對數(shù)坐標(biāo)系下真應(yīng)力與真塑性應(yīng)變的關(guān)系接近線性，因此可以用Hollomon公式(式2)描述兩者之間的關(guān)系

σ=K×ε˙m×εpn

(2)

其中σ、u2008u2008ε˙、εp分別為真應(yīng)力、應(yīng)變速率、真塑性應(yīng)變，K、m、n為材料參數(shù)，K為強(qiáng)度系數(shù)，m為應(yīng)變速率敏感因子，n為加工硬化指數(shù)

圖5



圖5Ti-6Al-4V軋制板材各向各層的室溫單調(diào)壓縮應(yīng)力應(yīng)變曲線

Fig.5Compressive stress-strain curves of the rolled Ti-6Al-4V plate at room temperature (a) true stress versus true strain and (b) true stress versus true plastic strain

使用式(1)對各應(yīng)力-應(yīng)變曲線的彈性段進(jìn)行線性擬合，斜率即為每個條件下的彈性模量E 根據(jù)擬合結(jié)果繪制出的直線向右平移0.2%的應(yīng)變量，則直線與應(yīng)力應(yīng)變曲線交點處的應(yīng)力即為名義屈服強(qiáng)度(σp0.2，下文用σy表達(dá)) 使用式(2)對塑性段在雙對數(shù)坐標(biāo)系下的真應(yīng)力-塑性應(yīng)變曲線進(jìn)行線性擬合，斜率即為每個條件下的加工硬化指數(shù)n，截距為lg(K×ε˙m) 應(yīng)變速率敏感因子m的取得，需要設(shè)計不同應(yīng)變速率下的單調(diào)壓縮實驗 由于本文的單調(diào)壓縮實驗均固定在同一個應(yīng)變速率0.8×10-4/s下，無法得到m，因此也無法得到K 單調(diào)壓縮實驗在總應(yīng)變達(dá)到4%左右時，即終止(圖5a)，此時試樣均未斷裂，因此也未測出單調(diào)壓縮的抗壓強(qiáng)度、斷后伸長率和斷面收縮率等性能指標(biāo) 得到的T i-6Al-4V軋制板材各向各層單調(diào)壓縮性能(σy, E, n)匯總于表1

由圖5和表1可以得出：隨著織構(gòu)的存在和變化，Ti-6Al-4V軋制板材單調(diào)壓縮性能出現(xiàn)顯著的各向異性和沿板厚方向的變化 關(guān)于各向異性，屈服強(qiáng)度σy和彈性模量E均表現(xiàn)為TD>RD>ND 沿板厚方向從表層到心部，<0001>晶向的取向由TD向RD逐漸發(fā)散，使TD試樣的屈服強(qiáng)度σy和彈性模量E均出現(xiàn)下降的趨勢，其中屈服強(qiáng)度σy的降幅可達(dá)60 MPa，而RD試樣的性能則呈現(xiàn)微弱的上升趨勢

從表1還可見，加工硬化指數(shù)n也因為織構(gòu)的出現(xiàn)及變化而出現(xiàn)一定的各向異性和沿板厚方向的變化 加工硬化指數(shù)n與<0001>峰值極密度之間有接近線性的正相關(guān)關(guān)系，因此加工硬化指數(shù)n是一個與宏觀織構(gòu)指標(biāo)<0001>峰值極密度緊密相關(guān)的力學(xué)性能指標(biāo)，可在一定程度上通過后者調(diào)控前者

2.1.3 室溫壓縮蠕變性能

圖6a、b分別給出了歸一化后蠕變應(yīng)力均為0.95σy時Ti-6Al-4V各向各層室溫壓縮蠕變的蠕變應(yīng)變-時間曲線和蠕變速率-時間曲線 由圖6b可見，蠕變速率ε˙c隨時間t呈不斷下降，說明在0.95σy的蠕變應(yīng)力水平下Ti-6Al-4V軋制板材前100 h的室溫壓縮蠕變基本上屬于初始蠕變階段 在雙對數(shù)坐標(biāo)系下蠕變速率ε˙c隨時間t的關(guān)系接近線性下降，說明兩者之間的關(guān)系可表示為

lgε˙c=c1lgt+c2

(3)

圖6



圖6Ti-6Al-4V軋制板材各向各層的室溫壓縮蠕變應(yīng)變-時間曲線以及蠕變速率-時間曲線

Fig. 6Compressive creep behavior of the rolled Ti-6Al-4V plate at creep stress of 0.95σy at room temperature (a) creep strain versus creep time and (b) creep strain rate versus creep time

解式(3)中的微分方程并根據(jù)邊界條件蠕變時間t=0和蠕變應(yīng)變εc=0，可得蠕變應(yīng)變εc與時間t之間的關(guān)系

εc=A×tb

(4)

式(4)已經(jīng)在鈦合金的室溫蠕變實驗中得到了驗證和使用[5~7,9,13,27,28]，其中蠕變參數(shù)A和b分別為蠕變系數(shù)和蠕變指數(shù)，擬合圖6a中的蠕變應(yīng)變-時間曲線可得 表2列出了本文所用的Ti-6Al-4V軋制板材各向各層室溫壓縮蠕變參數(shù)的擬合結(jié)果(擬合時蠕變應(yīng)變、時間分別以%、h為單位)

Table 2

表2

表2Ti-6Al-4V各向各層室溫壓縮蠕變參數(shù)的擬合結(jié)果(平行樣數(shù)量為2)

Table 2Fitting results of creep parameters during room temperature compressive creep of the rolled Ti-6Al-4V plate (the number of parallel samples is 2)

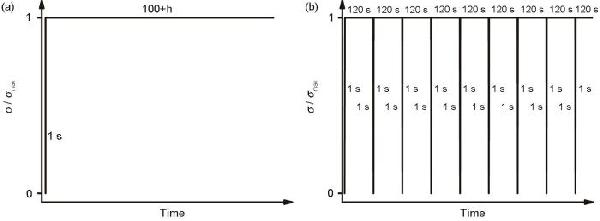
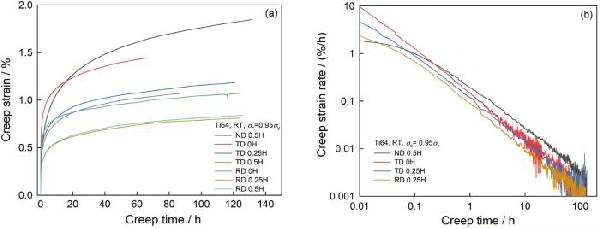
	Creep coefficient A	Creep exponent b	<0001> peak pole density
ND 0.5H	0.82	0.17	-
TD 0H	0.87	0.13	3.15
TD 0.25H	0.71	0.13	2.08
TD 0.5H	0.49	0.12	5
RD 0H	0.39	0.17	-
RD 0.25H	0.52	0.16	1.28
RD 0.5H	0.39	0.16	2.08

進(jìn)行理論推導(dǎo)[7,13]可得蠕變參數(shù)A、b與其他材料參數(shù)和實驗參數(shù)的關(guān)系為

A=(σcK)1m+n×(m+nm)mm+n

(5)

b=mm+n

(6)

其中m、n、K分別為材料的應(yīng)變速率敏感因子、加工硬化指數(shù)和強(qiáng)度系數(shù) 這三者可通過設(shè)計不同應(yīng)變速率下的恒應(yīng)變速率單調(diào)加載實驗得到[7] σc為蠕變應(yīng)力，意味著在理論上可通過恒應(yīng)變速率單調(diào)加載實驗得到材料參數(shù)m、n、K，然后使用公式(5)和(6)計算出公式(4)中的蠕變參數(shù)A和b，進(jìn)而計算并預(yù)測蠕變應(yīng)變-時間曲線 同時，公式(6)表明，材料的蠕變指數(shù)b只是材料參數(shù)m、n的函數(shù)，因此b也是材料參數(shù)，且隨著n的增大以及m的減小而減小 對于一定的材料，蠕變指數(shù)b不變，而蠕變系數(shù)A隨著蠕變應(yīng)力σc的增大而增大 這意味著，蠕變效應(yīng)隨蠕變應(yīng)力σc的增大而增大

由圖6a和表2可見：Ti-6Al-4V軋制板材室溫壓縮蠕變性能也出現(xiàn)顯著的各向異性和沿板厚方向的變化 在各向異性方面，對比板材心部(0.5H)的數(shù)據(jù)，ND試樣的蠕變系數(shù)A和蠕變指數(shù)b均大于TD和RD試樣 從表1可見，ND試樣的屈服強(qiáng)度σy最低，在歸一化蠕變應(yīng)力σc均為0.95σy的情況下，σc也是最低的 此時ND試樣的兩個蠕變參數(shù)A和b依舊最大，表明ND試樣的蠕變性能最差 而與RD試樣相比，TD試樣的情況略為復(fù)雜 在總體上，TD試樣的蠕變系數(shù)A較大，而蠕變指數(shù)b較小 從圖6a中的蠕變應(yīng)變-時間曲線可見，蠕變系數(shù)A較小的RD試樣的蠕變應(yīng)變量總體偏小，其蠕變性能看似更優(yōu)，但是從表1可見，TD試樣的屈服強(qiáng)度比RD試樣高50~100 MPa 在歸一化后蠕變應(yīng)力均為0.95σy的情況下，TD試樣的蠕變應(yīng)力仍高出RD試樣近48~95 MPa 而公式(5)表明，蠕變系數(shù)A是一個與蠕變應(yīng)力σc相關(guān)的物理量，因此TD試樣的蠕變系數(shù)較大，相同時間條件下其蠕變量更高是正常的，并不能因此認(rèn)定TD試樣的蠕變性能更差

應(yīng)在相同的使役條件下評價兩種材料某種性能的優(yōu)劣，例如在相同的蠕變應(yīng)力值下評價兩種材料的蠕變性能 因此，本文歸一化蠕變應(yīng)力的實驗設(shè)計，直接使用與蠕變應(yīng)力σc相關(guān)的蠕變系數(shù)A或蠕變量評價不同方向試樣蠕變性能的優(yōu)劣是不妥的 而公式(6)表明，蠕變指數(shù)b是一個與蠕變應(yīng)力σc無關(guān)的材料參數(shù)，只與材料參數(shù)m、n相關(guān) 同時，考慮到蠕變性能是材料在較長服役時間中的表現(xiàn)，蠕變指數(shù)b作為蠕變量增長的衡量指標(biāo)(雙對數(shù)坐標(biāo)系下蠕變應(yīng)變-時間曲線的斜率)，對更長時間后的蠕變量更具有決定性 更小的蠕變指數(shù)b往往代表更優(yōu)的蠕變性能 因此在蠕變應(yīng)力值σc不統(tǒng)一的情況下，應(yīng)該使用與蠕變應(yīng)力值不相關(guān)的材料參數(shù)蠕變指數(shù)b評價材料的蠕變性能 從蠕變指數(shù)b的角度評價蠕變性能，TD試樣的蠕變指數(shù)b更小，其蠕變性能更優(yōu)，這與TD試樣比RD和ND試樣具有更高的<0001>峰值極密度以及更高的屈服強(qiáng)度σy、彈性模量E以及加工硬化指數(shù)n的結(jié)果相吻合

比較壓縮蠕變性能沿板厚方向的變化趨勢，可以發(fā)現(xiàn)，無論是TD還是RD，心部試樣的A、b均小于表層以及亞表層試樣 這表明，心部的蠕變性能優(yōu)于表層以及亞表層，而這個結(jié)果與無論是TD還是RD心部試樣均具有較高的<0001>峰值極密度是對應(yīng)的，見圖4和表2

從表1和表2可見，加工硬化指數(shù)n和蠕變指數(shù)b均與織構(gòu)指標(biāo)<0001>峰值極密度密切相關(guān)，因此可以綜合考慮三者之間的量化關(guān)系 從圖7a可見，隨著<0001>峰值極密度的增大材料的加工硬化指數(shù)n接近線性地增大，而蠕變指數(shù)b接近線性地降低(蠕變性能變優(yōu))，因此加工硬化指數(shù)n與蠕變指數(shù)b之間應(yīng)存在接近線性的關(guān)系(圖7b)，這似乎與公式(6)所示的n與b之間的非線性關(guān)系不符 圖7b給出了實測的加工硬化指數(shù)n與蠕變指數(shù)b之間的關(guān)系，和對m不同賦值時根據(jù)公式(6)計算出的加工硬化指數(shù)n與蠕變指數(shù)b之間的關(guān)系 可以看出，根據(jù)公式(6)計算出的加工硬化指數(shù)n與蠕變指數(shù)b之間的關(guān)系在局部范圍內(nèi)接近線性變化；還可以看出，當(dāng)m約為0.0075時根據(jù)公式(6)計算出的n-b之間的關(guān)系與實測結(jié)果比較接近 這在一定程度上表明了公式(6)的適用性，還能評估出Ti-6Al-4V的m約為0.0075 文獻(xiàn)[7]實測了Ti6242室溫壓縮時的m為0.01，而Ti6242的室溫蠕變量和蠕變指數(shù)b顯著比Ti-6Al-4V的大 公式(6)表明，b隨著m的減小而減小，因此Ti-6Al-4V的m值0.0075小于0.01是合理的 如果把m假設(shè)成一個固定值代入公式(6)是偏于理想化的，織構(gòu)的變化影響合金的加工硬化指數(shù)n，也可能影響其應(yīng)變速率敏感因子m 因此圖7b中的部分實測數(shù)據(jù)點，在一定程度上偏離把m賦值為0.0075代入公式(6)計算出的加工硬化指數(shù)n與蠕變指數(shù)b之間的關(guān)系

圖7



圖7加工硬化指數(shù)n和蠕變指數(shù)b與<0001>峰值極密度之間的關(guān)系

Fig.7Relationships between material constants and <0001> peak pole density (a) and relationship between work hardening exponent n and creep exponent b (b)

綜上所述，Ti-6Al-4V軋制板材中的織構(gòu)使合金的室溫蠕變性能產(chǎn)生各向異性，織構(gòu)沿板厚方向的變化也使合金的室溫蠕變性能沿板厚方向變化 合金在加載方向上的<0001>峰值極密度增高，則其加工硬化指數(shù)n接近線性地增大，而蠕變指數(shù)b接近線性地降低，室溫蠕變性能變優(yōu) 室溫蠕變性能與單調(diào)加載性能緊密相關(guān)，在一定程度上可根據(jù)材料的單調(diào)加載性能參數(shù)快速評估蠕變性能

2.1.4 室溫壓縮保載疲勞性能

在廣義上，鈦合金的室溫保載疲勞的塑性應(yīng)變累積也可歸于室溫蠕變的范疇[4] 本文簡要設(shè)計了不同方向試樣的室溫壓縮保載疲勞實驗，并與普通室溫壓縮蠕變中的塑性應(yīng)變累積規(guī)律進(jìn)行對比，如圖8所示 從圖8可見，室溫壓縮保載疲勞中塑性應(yīng)變的累積與室溫壓縮蠕變均屬于初始蠕變階段 使用公式(4)也可取得較好的擬合結(jié)果，得到的蠕變參數(shù)列于表3(擬合時蠕變應(yīng)變、時間分別以%、h為單位) 如表3所示，室溫壓縮保載疲勞的塑性應(yīng)變累積的參數(shù)b也表現(xiàn)出了TD<RD<ND的規(guī)律，與普通壓縮蠕變中蠕變參數(shù)b隨各個方向的變化規(guī)律一致，都隨著<0001>峰值極密度的增大而減小

圖8



圖8Ti-6Al-4V軋制板材在普通壓縮蠕變和壓縮保載疲勞中塑性應(yīng)變的累積

Fig.8Accumulation of plastic strain εp in the rolled Ti-6Al-4V plate during normal compressive creep and compressive dwell fatigue when σmax is 0.95σy at room temperature

Table 3

表3

表3Ti-6Al-4V軋制板材室溫壓縮保載疲勞中蠕變參數(shù)的擬合結(jié)果(平行樣數(shù)量為2)

Table 3Fitting results of creep parameters during room temperature compressive dwell fatigue of the rolled Ti-6Al-4V plate (the number of parallel samples is 2)

	Creep coefficient A	Creep exponent b
ND 0.5H	1.20	0.17
TD 0H	1.46	0.09
RD 0H	1.21	0.12

與普通室溫蠕變相比，引入了疲勞過程的室溫保載疲勞的蠕變系數(shù)A明顯偏大，而蠕變指數(shù)b較為接近 因此，保載疲勞的塑性應(yīng)變累積速率和累積量都明顯比普通蠕變的高(圖8) 這意味著，保載疲勞中的疲勞行為促進(jìn)了塑性應(yīng)變累積 這種現(xiàn)象當(dāng)在有疲勞裂紋產(chǎn)生的情況下，可能與疲勞裂紋尖端塑性區(qū)(Crack Tip Plastic Zone, CTPZ[34,35])有關(guān)[36] 疲勞裂紋尖端的塑性區(qū)可作為放射源釋放大量的位錯，進(jìn)而使蠕變加劇[9]，而蠕變產(chǎn)生的塑性應(yīng)變又加劇了疲勞損傷[14]，從而引發(fā)疲勞-蠕變的交互作用[18]，使保載疲勞比普通蠕變有更快的塑性應(yīng)變累積速率

2.2 應(yīng)力水平對室溫蠕變的影響

從公式(5)和(6)中蠕變應(yīng)力對蠕變參數(shù)的影響，不難理解應(yīng)力水平對室溫蠕變的影響：蠕變應(yīng)力σc越高，雖然蠕變指數(shù)b不變但是蠕變系數(shù)A增大，因此蠕變效應(yīng)越明顯

以往通常采用常規(guī)蠕變的方法測試蠕變應(yīng)力門檻值，即進(jìn)行多個應(yīng)力水平下的常規(guī)蠕變實驗直到找出發(fā)生蠕變的應(yīng)力水平 本文參考文獻(xiàn)[1]設(shè)計了一種階梯升力蠕變實驗，研究不同應(yīng)力水平下的蠕變情況并測試Ti-6Al-4V合金的蠕變應(yīng)力門檻值 階梯升力蠕變實驗，是用一支試樣進(jìn)行蠕變應(yīng)力隨時間呈階梯狀遞增的實驗 典型的階梯升力蠕變實驗的應(yīng)力-時間曲線(即加載曲線)和應(yīng)力-應(yīng)變曲線，分別如圖9a和b所示 圖9c和d分別給出了在拉伸和壓縮條件下階梯升力蠕變實驗中各個應(yīng)力水平下的蠕變曲線 實驗結(jié)果表明：對于Ti-6Al-4V軋制板材，無論拉伸還是壓縮，只有蠕變應(yīng)力水平超過0.8σy時才能觀察到蠕變效應(yīng)，即合金的蠕變應(yīng)力門檻值約為0.8σy；當(dāng)蠕變應(yīng)力大于0.85σy時，室溫蠕變效應(yīng)較為明顯；高于蠕變應(yīng)力門檻值時，室溫蠕變效應(yīng)隨應(yīng)力水平的增大而增大 根據(jù)上述結(jié)果，探討其他因素對室溫蠕變性能的影響時，為了觀測到明顯的蠕變數(shù)據(jù)以進(jìn)行量化研究，應(yīng)選擇高于0.8σy的蠕變應(yīng)力，本文選用0.95σy

圖9



圖9階梯升力蠕變實驗的設(shè)計以及Ti-6Al-4V軋制板材階梯升力蠕變實驗中各應(yīng)力水平下蠕變應(yīng)變隨時間的變化

Fig. 9Design of load-step-increasing creep experiment and the changes of creep strain with time under different stress levels in load-step-increasing creep experiment of the rolled Ti-6Al-4V plate at room temperature (a) loading diagram and (b) strain-stress curve of load-step-increasing creep experiment, (c) creep curves under different stress levels in one tensile load-step-increasing creep experiment, (d) creep curves under different stress levels in one compressive load-step-increasing creep experiment

2.3 預(yù)塑性應(yīng)變對室溫蠕變的影響

在階梯升力蠕變實驗后，附帶進(jìn)行了階梯降力蠕變實驗(圖10a中的紅圈部分)以考察預(yù)先進(jìn)行的高應(yīng)力水平下的蠕變對后續(xù)各個較低應(yīng)力水平下蠕變的影響 在階梯降力蠕變實驗中發(fā)現(xiàn)：在高應(yīng)力水平下已發(fā)生的蠕變強(qiáng)烈抑制后續(xù)較低應(yīng)力水平下的蠕變(圖10b)，經(jīng)歷過高應(yīng)力水平(如0.95σy)下的蠕變后，低應(yīng)力水平(如0.9/0.85/0.8σy)下的蠕變幾乎很難再產(chǎn)生蠕變應(yīng)變 這種抑制現(xiàn)象，在拉伸或者壓縮階梯降力蠕變實驗中都被發(fā)現(xiàn)

圖10



圖10預(yù)塑性應(yīng)變對Ti-6Al-4V軋制板材室溫蠕變性能的影響

Fig. 10Effect of pre-plastic-strain on room temperature creep properties of the rolled Ti-6Al-4V plate (a) loading diagram of the load-step-decreasing creep experiment (in the red circle), (b) creep curves under different stress levels in one tensile load-step-decreasing creep experiment, (c) the effect of once existed high stress on creep, (d) the effect of pre-plastic-strain on creep

針對“高應(yīng)力水平下已發(fā)生的蠕變對后續(xù)較低應(yīng)力水平下的蠕變有著很強(qiáng)的抑制”，本文提出兩種假設(shè)：1、在加載歷史中存在的高應(yīng)力可抑制較低應(yīng)力水平下的蠕變；2、加載歷史中在高應(yīng)力下長時間蠕變產(chǎn)生的較大的塑性應(yīng)變導(dǎo)致的加工硬化抑制較低應(yīng)力水平下的蠕變 針對假設(shè)1，本文設(shè)計一種“拉伸+蠕變”(Tension+Creep，簡記為T+C)的實驗(圖10c)，先拉伸至屈服強(qiáng)度，卸載后再進(jìn)行0.9σy應(yīng)力水平的蠕變 實驗結(jié)果表明，此時0.9σy應(yīng)力水平下的蠕變效應(yīng)依舊很明顯(如圖10c中藍(lán)色框線所標(biāo)注) 這表明，瞬時存在的高應(yīng)力(即使達(dá)到σy)也不能抑制較低應(yīng)力水平下的蠕變，即假設(shè)1不成立 因此，“高應(yīng)力水平下已發(fā)生的蠕變對后續(xù)較低應(yīng)力水平下的蠕變有著很強(qiáng)的抑制作用”的關(guān)鍵，不在于較高的應(yīng)力而在于長時間(導(dǎo)致的蠕變)，不在于應(yīng)力而在于(塑性)應(yīng)變 為了研究塑性應(yīng)變對合金后續(xù)室溫蠕變的影響，本文設(shè)計了不同預(yù)塑性應(yīng)變(量與類型)對后續(xù)蠕變影響的實驗，結(jié)果如圖10d所示，其中“蠕變預(yù)制塑性應(yīng)變+蠕變實驗”和“拉伸預(yù)制塑性應(yīng)變+蠕變實驗”分別簡記為“C+C”和“T+C” 實驗結(jié)果表明：無論單調(diào)拉伸預(yù)制的塑性應(yīng)變還是拉伸蠕變預(yù)制的塑性應(yīng)變，均能抑制合金后續(xù)的拉伸蠕變 預(yù)塑性應(yīng)變量越大則抑制作用越明顯，預(yù)塑性應(yīng)變量相近時單調(diào)拉伸預(yù)制的塑性應(yīng)變與拉伸蠕變預(yù)制的塑性應(yīng)變對后續(xù)蠕變的抑制效果接近 雖然預(yù)先存在的塑性應(yīng)變抑制合金后續(xù)的蠕變效應(yīng)而使鈦合金結(jié)構(gòu)件后續(xù)使用過程中的尺寸穩(wěn)定性提高，但是預(yù)先存在的塑性應(yīng)變會惡化鈦合金材料的疲勞性能[14] 因此對于疲勞載荷下服役的鈦合金構(gòu)件，要綜合考慮預(yù)塑性應(yīng)變對材料室溫蠕變性能和疲勞性能的矛盾性影響

2.4 室溫蠕變對合金后續(xù)疲勞性能的影響

為了研究室溫蠕變產(chǎn)生的塑性應(yīng)變對Ti-6Al-4V后續(xù)疲勞性能的影響，本文設(shè)計了蠕變+三角波高周疲勞(C+HCF，見圖11a)與普通三角波高周疲勞(HCF)的對比實驗，為了對比拉伸蠕變預(yù)制的塑性應(yīng)變和單調(diào)拉伸預(yù)制的塑性應(yīng)變對合金疲勞性能影響的差異，還進(jìn)行了單調(diào)拉伸+三角波高周疲勞(T+HCF，見圖11b)的實驗 這些對比實驗中高周疲勞(HCF)的參數(shù)均為：σmax=0.8σy或0.95σy，應(yīng)力比R=0，拉應(yīng)力狀態(tài)，疲勞波形為三角波，疲勞頻率f為10 Hz 所有對比實驗的結(jié)果，都列于表4

圖11



圖11典型的“蠕變+疲勞”和“單調(diào)拉伸+疲勞”的應(yīng)力應(yīng)變曲線

Fig.11Typical strain-stress curves of Creep+HCF (a) and Tension+HCF (b)

Table 4

表4

表4預(yù)塑性應(yīng)變對Ti-6Al-4V軋制板材疲勞性能的影響

Table 4Effect of pre-plastic-strain on fatigue property of the rolled Ti-6Al-4V plate (R=0, f=10 Hz, triangular waveform, tensile stress)

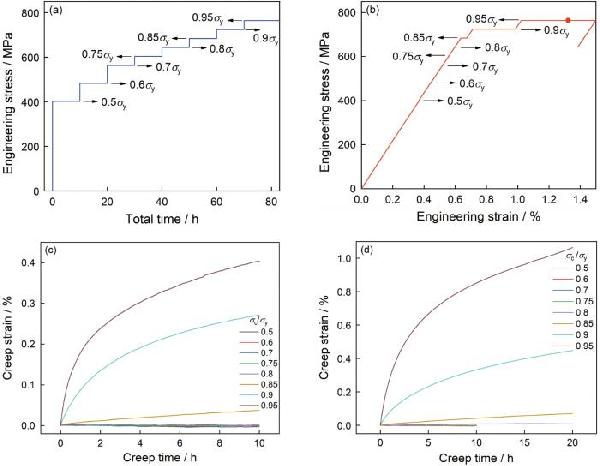
	σmax/σy	εp0/%	Nf
HCF	0.80	0	462055
HCF	0.80	0	444641
C+HCF	0.80	0.80	52881
T+HCF	0.80	0.98	48913
HCF	0.95	0	33952
HCF	0.95	0	31077
T+HCF	0.95	1.00	22570
C+HCF	0.95	1.37	16987

從表4可見，在疲勞參數(shù)相同的條件下，含有預(yù)塑性應(yīng)變的疲勞T+HCF和C+HCF與無預(yù)塑性應(yīng)變的普通疲勞HCF相比，疲勞壽命會明顯降低 在較低的疲勞峰值應(yīng)力σmax=0.8σy條件下，僅約為1%的預(yù)塑性應(yīng)變即可造成疲勞壽命(斷裂周次, Nf)將近10倍的下降；而在較高的疲勞峰值應(yīng)力σmax=0.95σy條件下，預(yù)塑性應(yīng)變造成的疲勞壽命降低的幅度略小，約為1%的預(yù)塑性應(yīng)變也可造成疲勞壽命近2倍的下降 上述實驗結(jié)果表明，蠕變或拉伸預(yù)制的塑性應(yīng)變均能降低材料的后續(xù)疲勞性能，且兩者在相近的預(yù)塑性應(yīng)變量的條件下對疲勞壽命的降低較為接近 因此，對于易于發(fā)生室溫蠕變的鈦合金，如果要應(yīng)用在包含疲勞的條件下，比如保載疲勞這種會發(fā)生疲勞-蠕變交互作用的條件下，需要充分考慮材料可能發(fā)生的室溫蠕變以及這些蠕變應(yīng)變對材料后續(xù)疲勞性能的影響 關(guān)于塑性應(yīng)變對鈦合金疲勞壽命的損害作用及機(jī)制，文獻(xiàn)[14]指出：試樣中存在的更大的塑性應(yīng)變意味著更高的位錯等缺陷密度以及拉向?qū)嶒炛懈叩恼鎽?yīng)力，這些因素使試樣在經(jīng)歷疲勞載荷時內(nèi)部產(chǎn)生更為劇烈的位錯等缺陷之間的交互作用，使疲勞損傷速率提高而使疲勞壽命降低

3 結(jié)論

(1) 宏觀織構(gòu)顯著影響Ti-6Al-4V合金的室溫蠕變性能 在加載方向上合金的<0001>峰值極密度越高，則其加工硬化指數(shù)n越大，蠕變指數(shù)b越小，室溫蠕變性能越好

(2) 只有當(dāng)蠕變應(yīng)力不小于0.85σy時才能觀察到Ti-6Al-4V軋制板材較為明顯的室溫蠕變，且室溫蠕變效應(yīng)隨著蠕變應(yīng)力水平的提高而增大

(3) 預(yù)塑性應(yīng)變能抑制合金后續(xù)的蠕變行為，預(yù)塑性應(yīng)變越大其抑制作用越明顯 已經(jīng)發(fā)生的蠕變應(yīng)變雖然能抑制合金后續(xù)的蠕變，但是也使合金后續(xù)的疲勞性能惡化

參考文獻(xiàn)

View Option 原文順序文獻(xiàn)年度倒序文中引用次數(shù)倒序被引期刊影響因子

[1]

Peng J, Zhou C Y, Dai Q, et al.

The temperature and stress dependent primary creep of CP-Ti at low and intermediate temperature

[J]. Mater. Sci. Eng., 2014, 611A: 123

[本文引用: 9]

[2]

Yamada T, Kawabata K, Sato E, et al.

Presences of primary creep in various phase metals and alloys at ambient temperature

[J]. Mater. Sci. Eng., 2004, 387-389A: 719

[本文引用: 3]

[3]

Kameyama T, Matsunaga T, Sato E, et al.

Suppression of ambient-temperature creep in CP-Ti by cold-rolling

[J]. Mater. Sci. Eng., 2009, 510-511A: 364

[4]

Harrison W J, Whittaker M T, Lancaster R J.

A model for time dependent strain accumulation and damage at low temperatures in Ti-6Al-4V

[J]. Mater. Sci. Eng., 2013, 574A: 130

[本文引用: 1]

[5]

Odegard B C, Thompson A W.

Low temperature creep of Ti-6Al-4V

[J]. Metall. Trans., 1974, 5: 1207

[本文引用: 5]

[6]

Thompson A W, Odegard B C.

The influence of microstructure on low temperature creep of Ti-5Al-2.5 Sn

[J]. Metall. Trans., 1973, 4: 899

[本文引用: 1]

[7]

Neeraj T, Hou D H, Daehn G S, et al.

Phenomenological and microstructural analysis of room temperature creep in titanium alloys

[J]. Acta Mater., 2000, 48: 1225

[本文引用: 9]

[8]

Imam M A, Gilmore C M.

Room temperature creep of Ti-6AI-4V

[J]. Metall. Trans., 1979, 10A: 419

[本文引用: 1]

[9]

Miller W H, Chen R T, Starke E A.

Microstructure, creep, and tensile deformation in Ti-6Al-2Nb-1Ta-0.8Mo

[J]. Metall. Trans., 1987, 18A: 1451

[本文引用: 9]

[10]

Doraiswamy D, Ankem S.

The effect of grain size and stability on ambient temperature tensile and creep deformation in metastable beta titanium alloys

[J]. Acta Mater., 2003, 51: 1607

[本文引用: 2]

[11]

Ramesh A, Ankem S.

The effect of grain size on the ambient temperature creep deformation behavior of a beta Ti-14.8 V alloy

[J]. Metall. Mater. Trans., 2002, 33A: 1137

[本文引用: 1]

[12]

Tanaka H, Yamada T, Sato E, et al.

Distinguishing the ambient-temperature creep region in a deformation mechanism map of annealed CP-Ti

[J]. Scripta Mater., 2006, 54: 121

[本文引用: 1]

[13]

Kassner M E, Smith K.

Low temperature creep plasticity

[J]. J. Mater. Res. Technol., 2014, 3: 280

[本文引用: 4]

[14]

Xi G Q, Lei J F, Qiu J K, et al.

A semi-quantitative explanation of the cold dwell effect in titanium alloys

[J]. Mater. Des., 2020, 194: 108909

[本文引用: 6]

[15]

Zhang Z.

Micromechanistic study of textured multiphase polycrystals for resisting cold dwell fatigue

[J]. Acta Mater., 2018, 156: 254

[本文引用: 2]

[16]

Bache M R.

A review of dwell sensitive fatigue in titanium alloys: the role of microstructure, texture and operating conditions

[J]. Int. J. Fatigue, 2003, 25: 1079

[本文引用: 3]

[17]

Qiu J K, Ma Y J, Lei J F, et al.

A comparative study on dwell fatigue of Ti-6Al-2Sn-4Zr-xMo (x=2 to 6) alloys on a microstructure-normalized basis

[J]. Metall. Mater. Trans., 2014, 45A: 6075

[本文引用: 2]

[18]

Sun C Q, Li Y Q, Xu K L, et al.

Effects of intermittent loading time and stress ratio on dwell fatigue behavior of titanium alloy Ti-6Al-4V ELI used in deep-sea submersibles

[J]. J. Mater. Sci. Technol., 2021, 77: 223

[本文引用: 2]

[19]

Evans W J, Gostelow C R.

The effect of hold time on the fatigue properties of a β-processed titanium alloy

[J]. Metall. Trans., 1979, 10A: 1837

[20]

Gerland M, Lefranc P, Doquet V, et al.

Deformation and damage mechanisms in an α/β 6242 Ti alloy in fatigue, dwell-fatigue and creep at room temperature. Influence of internal hydrogen

[J]. Mater. Sci. Eng., 2009, 507A: 132

[21]

Kassner M E, Kosaka Y, Hall J S.

Low-cycle dwell-time fatigue in Ti-6242

[J]. Metall. Mater. Trans., 1999, 30A: 2383

[本文引用: 1]

[22]

Andenstedt H.

Creep of titanium at room temperature

[J]. Metal Prog., 1949, 56: 658

[本文引用: 1]

[23]

Ankem S, Wyatt Z W, Joost W.

Advances in low-temperature (<0.25Tm) creep behavior of single and two-phase titanium alloys

[J]. Proced. Eng., 2013, 55: 10

[本文引用: 1]

[24]

Aiyangar A K, Neuberger B W, Oberson P G, et al.

The effects of stress level and grain size on the ambient temperature creep deformation behavior of an alpha Ti-1.6 wt pct V alloy

[J]. Metall. Mater. Trans., 2005, 36A: 637

[本文引用: 2]

[25]

Jaworski A, Ankem P S.

Influence of the second phase on the room-temperature tensile and creep deformation mechanisms of α-β titanium alloys, Part II: Creep deformation

[J]. Metall. Mater. Trans., 2006, 37A: 2755

[本文引用: 1]

[26]

Wyatt Z W, Ankem S.

Advances in low temperature (<0.25Tm) creep deformation mechanisms of alpha

alpha plus beta, and beta titanium alloys [A].Proceedings of the Ti-2011: Proceedings of the 12th World Conference on Titanium, Vol II [C]. 2012: 862

[本文引用: 1]

[27]

Zhang W D, Liu Y, Wu H, et al.

Room temperature creep behavior of Ti-Nb-Ta-Zr-O alloy

[J]. Mater. Charact., 2016, 118: 29

[本文引用: 2]

[28]

Hultgren C A, Ankem S, Greene C A.

Time-dependent twinning during ambient temperature compression creep of alpha Ti-0. 4Mn alloy

[J]. Metall. Mater. Trans., 1999, 30A: 1675

[本文引用: 2]

[29]

Wang Y N, Huang J C.

Texture analysis in hexagonal materials

[J]. Mater. Chem. Phys., 2003, 81: 11

[本文引用: 1]

[30]

Li W Y, Liu J R, Chen Z Y, et al.

Effect of microstructure and texture on room temperature strength of Ti60 Ti-alloy plate

[J]. Chin. J. Mater. Res., 2018, 32: 455

[本文引用: 1]

李文淵, 劉建榮, 陳志勇等.

Ti60合金板材的室溫強(qiáng)度與其顯微組織和織構(gòu)的關(guān)系

[J]. 材料研究學(xué)報, 2018, 32: 455

[本文引用: 1]

[31]

Hasija V, Ghosh S, Mills M J, et al.

Deformation and creep modeling in polycrystalline Ti-6Al alloys

[J]. Acta Mater., 2003, 51: 4533

[本文引用: 1]

[32]

Cuddihy M A, Stapleton A, Williams S, et al.

On cold dwell facet fatigue in titanium alloy aero-engine components

[J]. Int. J. Fatigue, 2017, 97: 177

[33]

Zheng Z B, Balint D S, Dunne F P E.

Mechanistic basis of temperature-dependent dwell fatigue in titanium alloys

[J]. J. Mech. Phys. Solids, 2017, 107: 185

[本文引用: 1]

[34]

Ma Y J, Xue Q, Wang H, et al.

Deformation twinning in fatigue crack tip plastic zone of Ti-6Al-4V alloy with widmanstatten microstructure

[J]. Mater. Charact., 2017, 132: 338

[本文引用: 1]

[35]

Ma Y J, Youssef S S, Feng X, et al.

Fatigue crack tip plastic zone of αu202f+u202fβ titanium alloy with widmanstatten microstructure

[J]. J. Mater. Sci. Technol., 2018, 34: 2107

[本文引用: 1]

[36]

Dai Q, Zhou C Y, Peng J, et al.

Room-temperature creep behavior on crack tip of commercially pure titanium

[J]. Mater. Des., 2015, 85: 618

[本文引用: 1]

The temperature and stress dependent primary creep of CP-Ti at low and intermediate temperature

9

2014